Anders Wikum

I am a fourth year PhD Candidate in Management Science & Engineering at Stanford University, advised by Ellen Vitercik. Broadly, my research studies how machine learning predictions or other distributional information can be used to improve decision-making in uncertain environments.
Prior to Stanford, I earned a B.S. in Operations Research from Cornell University before spending a year in Boston as a consultant/data scientist at QuantumBlack. My work was previously supported by a 2022 National Defense Science & Engineering Graduate (NDSEG) fellowship.
selected publications
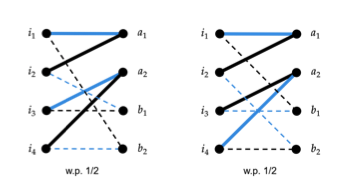
- Optimal Rounding for Two-Stage Bipartite MatchingIn Symposium on Discrete Algorithms (SODA), 2026
Two-stage bipartite matching is a fundamental model of batched matching: the aim is to compute a high-weight matching in a graph whose edges are revealed in two stages. One must commit to a partial matching in stage 1 without knowledge of the second-stage graph, before completing the matching in stage 2. Previous work gave a 0.761-approximation to the optimal online algorithm under a structured second-stage distribution. We improve this guarantee to 0.875 for vertex-weighted graphs and 0.828 for edge-weighted graphs under arbitrary distributions. Both approximation bounds are tight in the sense that they match the integrality gap of the natural linear programming relaxation.
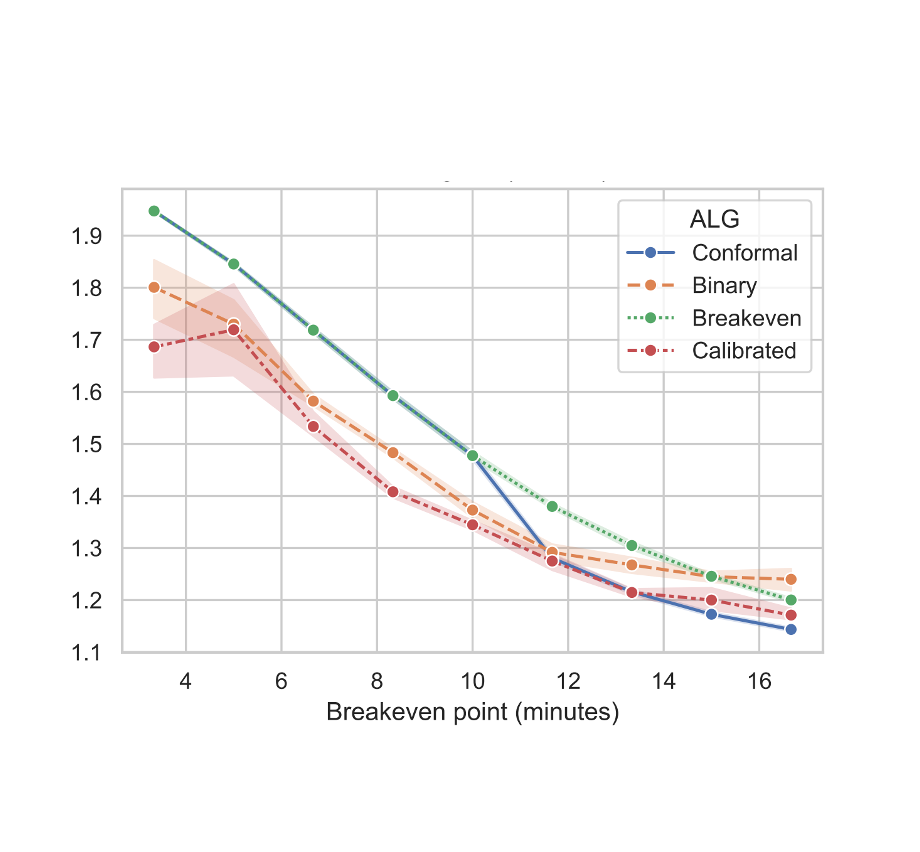
- Algorithms with Calibrated Machine Learning PredictionsIn International Conference on Machine Learning (ICML), 2025
A central question in the design of learning-augmented algorithms is the extent to which ML predictions can be trusted. Existing approaches often require users to specify an aggregate trust level (e.g. a bound on worst-case prediction error). In constrast, we leverage calibration—a widely used measure of ML reliability—to design algorithms with stronger, data-driven performance guarantees. This approach preserves worst-case robustness while allowing performance to adaptively improve with prediction quality.
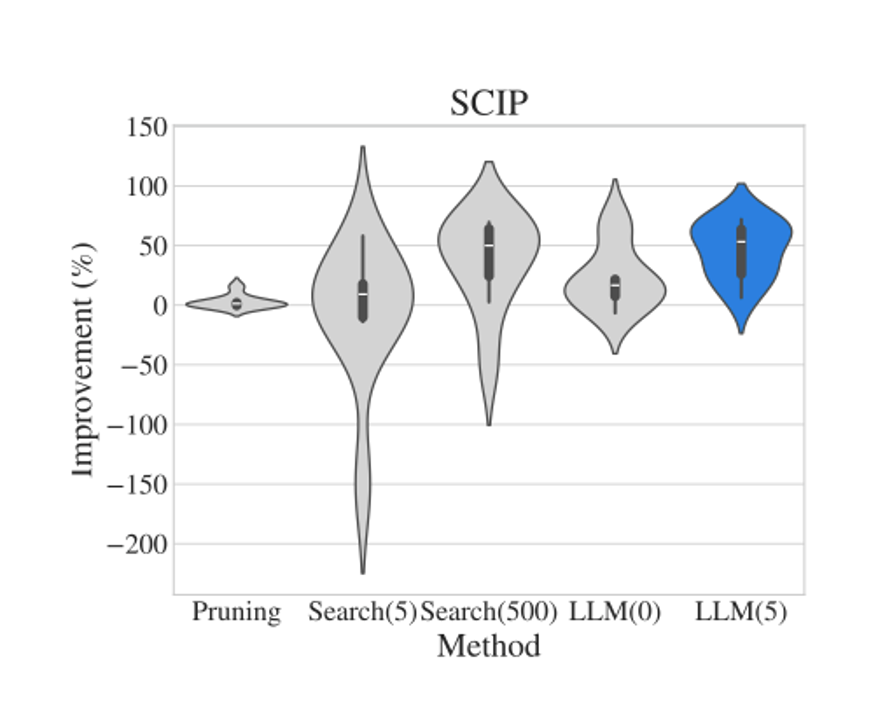
- LLMs for Cold-Start Cutting Plane Separator ConfigurationIn International Conference on the Integration of Constraint Programming, Artificial Intelligence, and Operations Research (CPAIOR), 2024
Cutting planes are an essential tool for solving mixed-integer linear programs (MILPs), but determining which cut families to apply to a particular problem formulation is a challenge even for optimization experts. In this paper, we develop a framework to elicit, and extract signals from, LLM cut recommendations. Notably, we find that our approach matches or outperforms existing ML-based approaches for cut configuration at a fraction of the cost.
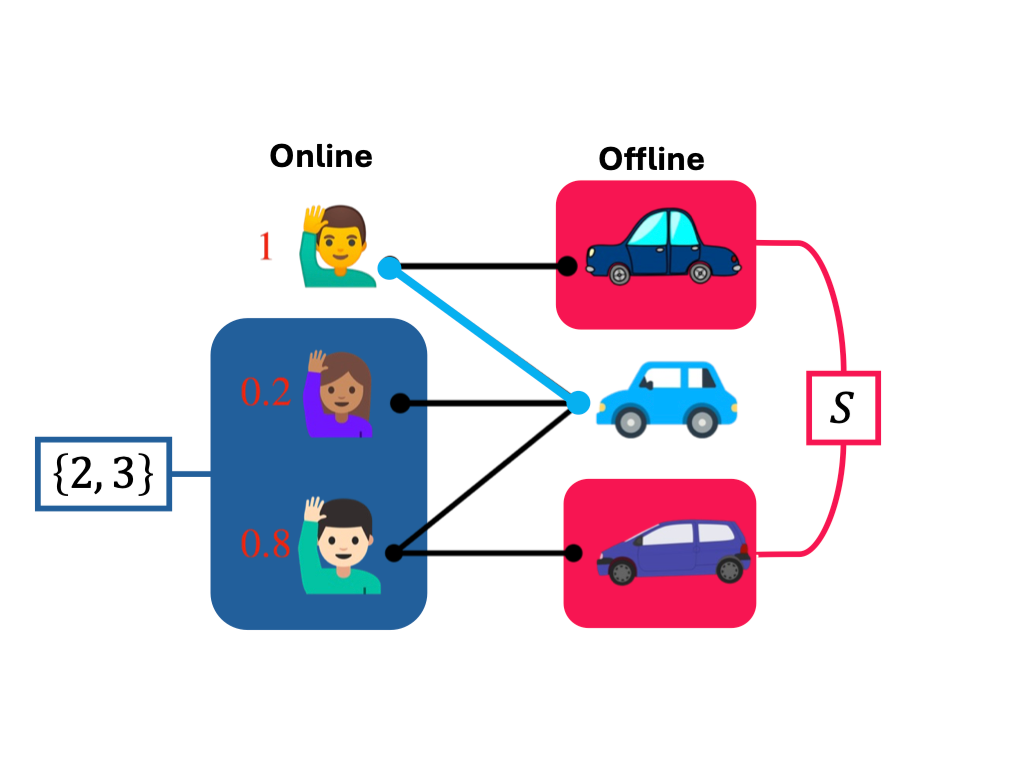
- MAGNOLIA: Matching Algorithms via GNNs for Online Value-to-go ApproximationIn International Conference on Machine Learning (ICML), 2024
ML approaches for online matching generally attempt to learn a value-to-go (VTG) function, or the long-term utility associated with each matching decision. We study a matching model in which VTG solves an exponential-size Bellman equation. Despite a hardness of approximation result, we show empirically that graph neural networks (GNNs) trained to predict VTG are able to recover near-optimal matching policies for many practical graph families. A theoretical analysis supports our findings by showing that the VTG function is approximately local on a broad class of geometric graphs.